Guida al Visual Basic .NET
Capitolo 36° - Classi Astratte Sigillate e Parziali
Classi AstratteLe classi astratte sono speciali classi che esistono con il solo scopo di essere ereditate da altre classi: non possono essere usate da sole, non espongono costruttori e alcuni loro metodi sono privi di un corpo. Queste sono caratteristiche molto peculiari, e anche abbastanza strane, che, tuttavia, nascondono un potenziale segreto. Se qualcuno dei miei venticinque lettori avesse avuto l'occasione di osservare qualcuno dei miei sorgenti, avrebbe notato che in più di un occasione ho fatto uso di classi marcate con la keyword MustInherit. Questa è la parola riservata che si usa per rendere astratta una classe. L'utilizzo principale delle classi astratte è quello di fornire uno scheletro o una base di astrazione per altre classi. Prendiamo come esempio uno dei miei programmi, che potete trovare nella sezione download, Totem Charting: ci riferiremo al file Chart.vb. In questo sorgente, la prima classe che incontrate è definita come segue:<Serializable()> _ Public MustInherit Class ChartPer ora lasciamo perdere ciò che viene compreso tra le parentesi angolari e focalizziamoci sulla dichiarazione nuda e cruda. Quella che avete visto è proprio la dichiarazione di una classe astratta, dove MustInherit significa appunto "deve ereditare", come riportato nella definizione poco sopra. Chart rappresenta un grafico: espone delle proprietà (Properties, Type, Surface, Plane, ...) e un paio di metodi Protected. Sarete d'accordo con me nell'asserire che ogni grafico può avere una legenda e può contemplare un insieme di dati limitato per cui esista un massimo: ne concludiamo che i due metodi in questione servono a tutti i grafici ed è corretto che siano stati definiti all'interno del corpo di Chart. Ma ora andiamo un po' più in su e troviamo questa singolare dichiarazione di metodo: Public MustOverride Sub Draw()Non c'è il corpo del metodo! Aiuto! L'hanno rubato! No... Si dà il caso che nelle classi astratte possano esistere anche metodi astratti, ossia che devono essere per forza ridefiniti tramite polimorfismo nelle classi derivate. E questo è abbastanza semplice da capire: un grafico deve poter essere disegnato, quindi ogni oggetto grafico deve esporre il metodo Draw, ma c'è un piccolo inconveniente. Dato che non esiste un solo tipo di grafico - ce ne sono molti, e nel codice di Totem Charting vengono contemplati solo gli istogrammi, gli areaogrammi e i grafici a dispersione - non possiamo sapere a priori che codice dovremmo usare per effettuare il rendering (ossia per disegnare ciò che serve). Sappiamo, però, che dovremo disegnare qualcosa: allora lasciamo il compito di definire un codice adeguato alle classi derivate (nella fattispecie, Histogram, PieChart, LinesChart, DispersionChart). Questo è proprio l'utilizzo delle classi astratte: definire un archetipo, uno schema, sulla base del quale le classi che lo erediteranno dovranno modellare il proprio comportamento. Altra osservazione: le classi astratte, come dice il nome stesso, sono utilizzate per rappresentare concetti astratti, che non possono concretamente essere istanziati: ad esempio, non ha senso un oggetto di tipo Chart, perchè non esiste un grafico generico privo di qualsiasi caratteristica, ma esiste solo declinato in una delle altre forme sopra riportate. Naturalmente, valgono ancora tutte le regole relative agli specificatori di accesso e all'ereditarietà e sono utilizzabili tutti i meccanismi già illustrati, compreso l'overloading; infatti, ho dichiarato due metodi Protected perchè serviranno alle classi derivate. Inoltre, una classe astratta può anche ereditare da un'altra classe astratta: in questo caso, tutti i metodi marcati con MustOverride dovranno subire una di queste sorti:
Module Module1
'Classe astratta che rappresenta un risolutore di equazioni.
'Dato che di equazioni ce ne possono essere molte tipologie
'differenti, non ha senso rendere questa classe istanziabile.
'Provando a scrivere qualcosa come:
' Dim Eq As New EquationSolver()
'Vi verrà comunicato un errore, in quanto le classi
'astratte sono per loro natura non istanziabili
MustInherit Class EquationSolver
'Per lo stesso discorso fatto prima, se non conosciamo come
'è fatta l'equazione che questo tipo contiene non
'possiamo neppure tentare di risolverla. Perciò
'ci limitiamo a dichiarare una funzione Solve come MustOverride.
'Notate che il tipo restituito è un array di Single,
'in quanto le soluzioni saranno spesso più di una.
Public MustOverride Function Solve() As Single()
End Class
'La prossima classe rappresenta un risolutore di equazioni
'polinomiali. Dato che la tipologia è ben definita,
'avremmo potuto anche non rendere astratta la classe
'e, nella funzione Solve, utilizzare un Select Case per
'controllare il grado dell'equazione. Ad ogni modo, è
'utile vedere come si comporta l'erediterietà attraverso
'più classi astratte.
'Inoltre, ci ritornerà molto utile in seguito disporre
'di questa classe astratta intermedia
MustInherit Class PolynomialEquationSolver
Inherits EquationSolver
Private _Coefficients() As Single
'Array di Single che contiene i coefficienti dei
'termini di i-esimo grado all'interno dell'equazione.
'L'elemento 0 dell'array indica il coefficiente del
'termine a grado massimo.
Public Property Coefficients() As Single()
Get
Return _Coefficients
End Get
Set(ByVal value As Single())
_Coefficients = value
End Set
End Property
'Ecco quello a cui volevo arrivare. Se un metodo astratto
'lo si vuole mantenere tale anche nella classe derivata,
'non basta scrivere:
' MustOverride Function Solve() As Single()
'Percè in questo caso verrebbe interpretato come
'un membro che non c'entra niente con MyBase.Solve,
'e si genererebbe un errore in quanto stiamo tentando
'di dichiarare un nuovo membro con lo stesso nome
'di un membro della classe base.
'Per questo motivo, dobbiamo comunque usare il polimorfismo
'come se si trattasse di un normale metodo e dichiararlo
'Overrides. In aggiunta a questo, deve anche essere
'astratto, e perciò aggiungiamo MustOverride:
Public MustOverride Overrides Function Solve() As Single()
'Anche in questo caso usiamo il polimorfismo, ma ci riferiamo
'alla semplice funzione ToString, derivata dalla classe base
'di tutte le entità esistenti, System.Object.
'Questa si limita a restituire una stringa che rappresenta
'l'equazione a partire dai suoi coefficienti. Ad esempio:
' 3x^2 + 2x^1 + 4x^0 = 0
'Potete modificare il codice per eliminare le forme ridondanti
'x^1 e x^0.
Public Overrides Function ToString() As String
Dim Result As String = ""
For I As Int16 = 0 To Me.Coefficients.Length - 1
If I > 0 Then
Result &= " + "
End If
Result &= String.Format("{0}x^{1}", _
Me.Coefficients(I), Me.Coefficients.Length - 1 - I)
Next
Result &= " = 0"
Return Result
End Function
End Class
'Rappresenta un risolutore di equazioni non polinomiali.
'La classe non è astratta, ma non presenta alcun codice.
'Per risolvere questo tipo di equazioni, è necessario
'sapere qualche cosa in più rispetto al punto in cui siamo
'arrivati, perciò mi limiterò a lasciare in bianco
Class NonPolynomialEquationSolver
Inherits EquationSolver
Public Overrides Function Solve() As Single()
Return Nothing
End Function
End Class
'Rappresenta un risolutore di equazioni di primo grado. Eredita
'da PolynomialEquationSolver poichè, ovviamente, si
'tratta di equazioni polinomiali. In più, definisce
'le proprietà a e b che sono utili per inserire i
'coefficienti. Infatti, l'equazione standard è:
' ax + b = 0
Class LinearEquationSolver
Inherits PolynomialEquationSolver
Public Property a() As Single
Get
Return Me.Coefficients(0)
End Get
Set(ByVal value As Single)
Me.Coefficients(0) = value
End Set
End Property
Public Property b() As Single
Get
Return Me.Coefficients(1)
End Get
Set(ByVal value As Single)
Me.Coefficients(1) = value
End Set
End Property
'Sappiamo già quanti sono i coefficienti, dato
'che si tratta di equazioni lineari, quindi ridimensioniamo
'l'array il prima possibile.
Sub New()
ReDim Me.Coefficients(1)
End Sub
'Funzione Overrides che sovrascrive il metodo astratto della
'classe base. Avrete notato che quando scrivete:
' Inherits PolynomialEquationSolver
'e premete invio, questa funzione viene aggiunta automaticamente
'al codice. Questa è un'utile feature dell'ambiente
'di sviluppo
Public Overrides Function Solve() As Single()
If a <> 0 Then
Return New Single() {-b / a}
Else
Return Nothing
End If
End Function
End Class
'Risolutore di equazioni di secondo grado:
' ax2 + bx + c = 0
Class QuadraticEquationSolver
Inherits LinearEquationSolver
Public Property c() As Single
Get
Return Me.Coefficients(2)
End Get
Set(ByVal value As Single)
Me.Coefficients(2) = value
End Set
End Property
Sub New()
ReDim Me.Coefficients(2)
End Sub
Public Overrides Function Solve() As Single()
If b ^ 2 - 4 * a * c >= 0 Then
Return New Single() { _
(-b - Math.Sqrt(b ^ 2 - 4 * a * c)) / 2, _
(-b + Math.Sqrt(b ^ 2 - 4 * a * c)) / 2}
Else
Return Nothing
End If
End Function
End Class
'Risolutore di equazioni di grado superiore al secondo. So
'che avrei potuto inserire anche una classe relativa
'alle cubiche, ma dato che si tratta di un esempio, vediamo
'di accorciare il codice...
'Comunque, dato che non esiste formula risolutiva per
'le equazioni di grado superiore al quarto (e già,
'ci mancava un'altra classe!), usiamo in questo caso
'un semplice ed intuitivo metodo di approssimazione degli
'zeri, il metodo dicotomico o di bisezione (che vi può
'essere utile per risolvere un esercizio dell'eserciziario)
Class HighDegreeEquationSolver
Inherits PolynomialEquationSolver
Private _Epsilon As Single
Private _IntervalLowerBound, _IntervalUpperBound As Single
'Errore desiderato: l'algoritmo si fermerà una volta
'raggiunta una precisione inferiore a Epsilon
Public Property Epsilon() As Single
Get
Return _Epsilon
End Get
Set(ByVal value As Single)
_Epsilon = value
End Set
End Property
'Limite inferiore dell'intervallo in cui cercare la soluzione
Public Property IntervalLowerBound() As Single
Get
Return _IntervalLowerBound
End Get
Set(ByVal value As Single)
_IntervalLowerBound = value
End Set
End Property
'Limite superiore dell'intervallo in cui cercare la soluzione
Public Property IntervalUpperBound() As Single
Get
Return _IntervalUpperBound
End Get
Set(ByVal value As Single)
_IntervalUpperBound = value
End Set
End Property
'Valuta la funzione polinomiale. Dati i coefficienti immessi,
'noi disponiamo del polinomio p(x), quindi possiamo calcolare
'i valori che esso assume per ogni x
Private Function EvaluateFunction(ByVal x As Single) As Single
Dim Result As Single = 0
For I As Int16 = 0 To Me.Coefficients.Length - 1
Result += Me.Coefficients(I) * x ^ (Me.Coefficients.Length - 1 - I)
Next
Return Result
End Function
Public Overrides Function Solve() As Single()
Dim a, b, c As Single
Dim fa, fb, fc As Single
Dim Interval As Single = 100
Dim I As Int16 = 0
Dim Result As Single
a = IntervalLowerBound
b = IntervalUpperBound
'Non esiste uno zero tra a e b se f(a) e f(b) hanno
'lo stesso segno
If EvaluateFunction(a) * EvaluateFunction(b) > 0 Then
Return Nothing
End If
Do
'c è il punto medio tra a e b
c = (a + b) / 2
'Calcola f(a), f(b) ed f(c)
fa = EvaluateFunction(a)
fb = EvaluateFunction(b)
fc = EvaluateFunction(c)
'Se uno tra f(a), f(b) e f(c) vale zero, allora abbiamo
'trovato una soluzione perfetta, senza errori, ed
'usciamo direttamente dal ciclo
If fa = 0 Then
c = a
Exit Do
End If
If fb = 0 Then
c = b
Exit Do
End If
If fc = 0 Then
Exit Do
End If
'Altrimenti, controlliamo quale coppia di valori scelti
'tra f(a), f(b) ed f(c) ha segni discorsi: lo zero si troverà
'tra le ascisse di questi
If fa * fc < 0 Then
b = c
Else
a = c
End If
Loop Until Math.Abs(a - b) < Me.Epsilon
'Cicla finchè l'ampiezza dell'intervallo non è
'sufficientemente piccola, quindi assume come zero più
'probabile il punto medio tra a e b:
Result = c
Return New Single() {Result}
End Function
End Class
Sub Main()
'Contiene un generico risolutore di equazioni. Non sappiamo ancora
'quale tipologia di equazione dovremo risolvere, ma sappiamo per
'certo che lo dovremo fare, ed EquationSolver è la classe
'base di tutti i risolutori che espone il metodo Solve.
Dim Eq As EquationSolver
Dim x() As Single
Dim Cmd As Char
Console.WriteLine("Scegli una tipologia di equazione: ")
Console.WriteLine(" l - lineare;")
Console.WriteLine(" q - quadratica;")
Console.WriteLine(" h - di grado superiore al secondo;")
Console.WriteLine(" e - non polinomiale;")
Cmd = Console.ReadKey().KeyChar
Console.Clear()
If Cmd <> "e" Then
'Ancora, sappiamo che si tratta di un'equazione polinomiale
'ma non di quale grado
Dim Poly As PolynomialEquationSolver
'Ottiene i dati relativi a ciascuna equazione
Select Case Cmd
Case "l"
Dim Linear As New LinearEquationSolver()
Poly = Linear
Case "q"
Dim Quadratic As New QuadraticEquationSolver()
Poly = Quadratic
Case "h"
Dim High As New HighDegreeEquationSolver()
Dim CoefNumber As Int16
Console.WriteLine("Inserire il numero di coefficienti: ")
CoefNumber = Console.ReadLine
ReDim High.Coefficients(CoefNumber - 1)
Console.WriteLine("Inserire i limti dell'intervallo in cui cercare gli zeri:")
High.IntervalLowerBound = Console.ReadLine
High.IntervalUpperBound = Console.ReadLine
Console.WriteLine("Inserire la precisione (epsilon):")
High.Epsilon = Console.ReadLine
Poly = High
End Select
'A questo punto la variabile Poly contiene sicuramente un oggetto
'(LinearEquationSolver, QuadraticEquationSolver oppure
'HighDegreeEquationSolver), anche se non sappiamo quale. Tuttavia,
'tutti questi sono pur sempre polinomiali e perciò tutti
'hanno bisogno di sapere i coefficienti del polinomio.
'Ecco che allora possiamo usare Poly con sicurezza percè
'sicuramente contiene un oggetto e la proprietà Coefficients
'è stata definita proprio nella classe PolynomialEquationSolver.
'N.B.: ricordate tutto quello che abbiamo detto sull'assegnamento
' di un oggetto di classe derivata a uno di classe base!
Console.WriteLine("Inserire i coefficienti: ")
For I As Int16 = 1 To Poly.Coefficients.Length - 1
Console.Write("a{0} = ", Poly.Coefficients.Length - I)
Poly.Coefficients(I - 1) = Console.ReadLine
Next
'Assegnamo Poly a Eq. Osservate che siamo andati via via dal
'caso più particolare al più generale:
' - Abbiamo creato un oggetto specifico per un certo grado
' di un'equazione polinomiale (Linear, Quadratic, High);
' - Abbiamo messo quell'oggetto in uno che si riferisce
' genericamente a tutti i polinomi;
' - Infine, abbiamo posto quest'ultimo in uno ancora più
' generale che si riferisce a tutte le equazioni;
'Questo percorso porta da oggetto molto specifici e ricchi di membri
'(tante proprietà e tanti metodi), a tipi molto generali
'e poveri di membri (nel caso di Eq, un solo metodo).
Eq = Poly
Else
'Inseriamo in Eq un nuovo oggetto per risolvere equazioni non
'polinomiali, anche se il codice è al momento vuoto
Eq = New NonPolynomialEquationSolver
Console.WriteLine("Non implementato")
End If
'Risolviamo l'equazione. Richiamare la funzione Solve da un oggetto
'EquationSolver potrebbe non dirvi nulla, ma ricordate che dentro Eq
'è memorizzato un oggetto più specifico in cui
'è stata definita la funzione Solve(). Per questo motivo,
'anche se Eq è di tipo classe base, purtuttavia contiene
'al proprio interno un oggetto di tipo classe derivata, ed
'è questo che conta: viene usato il metodo Solve della classe
'derivata.
'Se ci pensate bene, vi verrà più spontaneo capire,
'poiché noi, ora, stiamo guardando ATTRAVERSO il tipo
'EquationSolver un oggetto di altro tipo. È come osservare
'attraverso filtri via via sempre più fitti (cfr
'immagine seguente)
x = Eq.Solve()
If x IsNot Nothing Then
Console.WriteLine("Soluzioni trovate: ")
For Each s As Single In x
Console.WriteLine(s)
Next
Else
Console.WriteLine("Nessuna soluzione")
End If
Console.ReadKey()
End Sub
End Module
Eccovi un'immagine dell'ultimo commento:
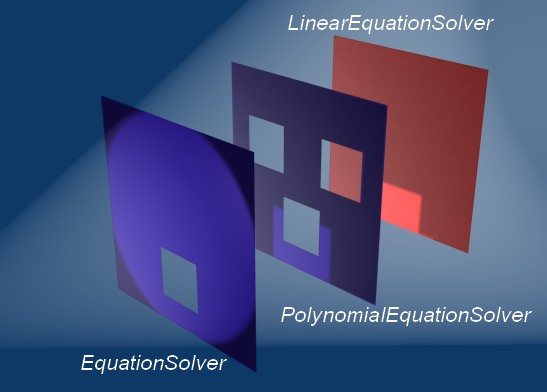 Il piano rosso è l'oggetto che realmente c'è in memoria (ad esempio, LinearEquationSolver); il piano blu con tre aperture è ciò che riusciamo a vedere quando l'oggetto viene memorizzato in una classe astratta PolynomialEquationSolver; il piano blu iniziale, invece, è ciò a cui possiamo accedere attraverso un EquationSolver: il fascio di luce indica le nostre possibilità di accesso. È proprio il caso di dire che c'è molto di più di ciò che si vede! Classi SigillateLe classi sigillate sono esattamente l'opposto di quelle astratte, ossia non possono mai essere ereditate. Si dichiarano con la keyword NotInheritable:NotInheritable Class Example
'...
End Class
Allo stesso modo, penserete voi, i membri che non possono subire overloading saranno marcati con qualcosa tipo NotOverridable... In parte
esatto, ma in parte errato. La keyword NotOverridable si può applicare solo e soltanto a metodi già modificati tramite
polimorfismo, ossia Overrides.
Class A
Sub DoSomething()
'...
End Sub
End Class
Class B
Inherits A
'Questa procedura sovrascrive la precedente versione
'di DoSomething dichiarata in A, ma preclude a tutte le
'classi derivate da B la possibilità di fare lo stesso
NotOverridable Overrides Sub DoSomething()
'...
End Sub
End Class
Inoltre, le classi sigillate non possono mai esporre membri sigillati, anche perchè tutti i loro membri lo sono implicitamente
(se una classe non può essere ereditata, ovviamente non si potranno ridefinire i membri con polimorfismo).Classi ParzialiUna classe si dice parziale quando il suo corpo è suddiviso su più files. Si tratta solamento di un'utilità pratica che ha poco a che vedere con la programmazione ad oggetti. Mi sembrava, però, ordinato esporre tutte le keyword associate alle classi in un solo capitolo. Semplicemente, una classe parziale si dichiara in questo modo:Partial Class [Nome]
'...
End Class
È sufficiente dichiarare una classe come parziale perchè il compilatore associ, in fase di assemblaggio, tutte le classi con lo
stesso nome in file diversi a quella definizione. Ad esempio:
'Nel file Codice1.vb :
Partial Class A
Sub One()
'...
End Sub
End Class
'Nel file Codice2.vb
Class A
Sub Two()
'...
End Sub
End Class
'Nel file Codice3.vb
Class A
Sub Three()
'...
End Sub
End Class
'Tutte le classi A vengono compilate come un'unica classe
'perchè una possiede la keyword Partial:
Class A
Sub One()
'...
End Sub
Sub Two()
'...
End Sub
Sub Three()
'...
End Sub
End Class
C#, TypeScript, java, php, EcmaScript (JavaScript), Spring, Hibernate, React, SASS/LESS, jade, python, scikit, node.js, redux, postgres, keras, kubernetes, docker, hexo, etc...
|

Il layout di questo sito è concesso sotto licenza Creative Commons.
Per informazioni sui contenuti visita la pagina delle licenze.
Sito gestito da MasseranoLabs LLC. Leggi l'informativa sui cookies.
Privacy Policy
Big-Bug.net ~ Programmazione ~ thetotalsite.it ~ Piero's Blog ~ Giochi ~ Altri... ~ Il tuo sito qui?

